サイクルタイムはより短く、スループットはより多く

☆リトルの法則の厳密な証明

まず、時刻０から時刻 $t$ までの、のべＷＩＰ数

$\Bigint_0^tWIP(\tau)d\tau$

を考えます。ここに $WIP(\tau)$ は時刻 $\tau$ の時のＷＩＰ数を表す関数とします。すると上記の積分は下図のオレンジ色で示した部分の面積を表していることになります。

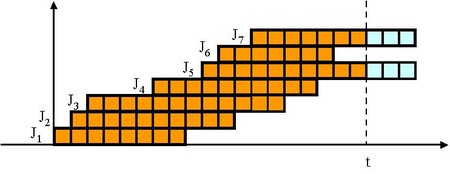
この図でジョブ $J_5$ よりあとに到着したジョブ $J_6$ が $J_5$ より先に終わっているのに注意して下さい。サイクルタイム（ $CT$ ）に変動があるために、このようなケースもあり得ることをこの図で考慮しています。

次に時刻０から時刻 $t$ までに到着したジョブのサイクルタイムの合計を考えます。この例の場合、時刻０から時刻 $t$ までに到着したジョブは $J_1$ 〜 $J_7$ です。よって、それらのジョブのサイクルタイムの合計は、下図のオレンジ色の部分の面積になります。

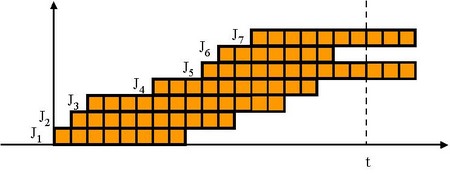
これを $Total-CT1(t)$ で表すことにします。

さらに時刻０から時刻 $t$ までに完了してラインから出ていったジョブのサイクルタイムの合計を考えます。この例の場合、時刻０から時刻 $t$ までに到着したジョブは $J_1$ 〜 $J_4$ と $J_6$ です。よって、それらのジョブのサイクルタイムの合計は、下図のオレンジ色の部分の面積になります。

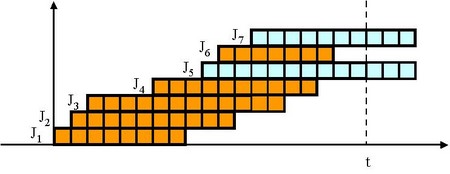
これを $Total-CT2(t)$ で表すことにします。

この３つの図を比べると、

$Total-CT2(t){\le}\Bigint_0^tWIP(\tau)d\tau{\le}Total-CT1(t)$

が成り立つことが分かります。この式を $t$ で割ると

$\frac{Total-CT2(t)}{t}{\le}\frac{1}{t}\times{\Bigint_0^tWIP(\tau)d\tau}{\le}\frac{Total-CT1(t)}{t}$

となります。ここでジョブの完了数を $C(t)$ とすると

$\frac{Total-CT1(t)}{t}=\frac{Total-CT1(t)}{C(t)}{\times}\frac{C(t)}{t}$

また、ジョブの到着数を $A(t)$ とすると

$\frac{Total-CT2(t)}{t}=\frac{Total-CT2(t)}{A(t)}{\times}\frac{A(t)}{t}$

ここで $t\rightar\infty$ とすると

$\frac{Total-CT1(t)}{C(t)}\rightar\bar{CT}$
$\frac{C(t)}{t}\rightar\bar{TH}$
$\frac{Total-CT2(t)}{C(t)}\rightar\bar{CT}$
$\frac{A(t)}{t}\rightar\bar{TH}$

となります。ただし $\bar{CT}$ は平均サイクルタイムを、 $\bar{TH}$ は平均スループットを表します。
よって

$\frac{Total-CT1(t)}{t}\rightar\bar{CT}{\times}\bar{TH}$
$\frac{Total-CT2(t)}{t}\rightar\bar{CT}{\times}\bar{TH}$

となります。
また、

$\frac{1}{t}\times{\Bigint_0^tWIP(\tau)d\tau}\rightar\bar{WIP}$

となります。ただし $\bar{WIP}$ は平均ＷＩＰを表します。

よって

$\frac{Total-CT2(t)}{t}{\le}\frac{1}{t}\times{\Bigint_0^tWIP(\tau)d\tau}{\le}\frac{Total-CT1(t)}{t}$

は

$\bar{CT}{\times}\bar{TH}{\le}\bar{WIP}{\le}\bar{CT}{\times}\bar{TH}$

となるので

$\bar{CT}{\times}\bar{TH}=\bar{WIP}$

となります。つまり

平均サイクルタイム×平均スループット＝平均ＷＩＰ

となります。これでリトルの法則の証明が出来ました。